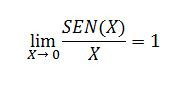MÁS SIMILITUDES ENTRE LÍMITES Y TICS

MÁS SIMILITUDES ENTRE LÍMITES Los siguientes límites tienen en común su forma: 1. Una función dividida entre X 2. La variable X tiende al valor 0 3. Su límite es: UNO Se muestran a continuación los ejemplos con sus correspondientes representaciones gráficas: A. FUNCIÓN SENO B. FUNCIÓN ARCO SENO C. FUNCIÓN LOGARÍTMO NATURAL D. FUNCIÓN EXPONENCIAL E. FUNCIÓN SENO HIPERBÓLICO A MANERA DE CONCLUSIÓN: Las TICS, con su dinamismo permiten a estudiantes y docentes explorar el comportamiento de los objetos matemáticos sin ninguna restricción, llevando a los dos a la apropiación racional de las ideas matemáticas. Siempre estoy trabajando por mostrar algo diferente! Nos vemos!