MODELACIÓN EN GEOMETRÍA DINÁMICA
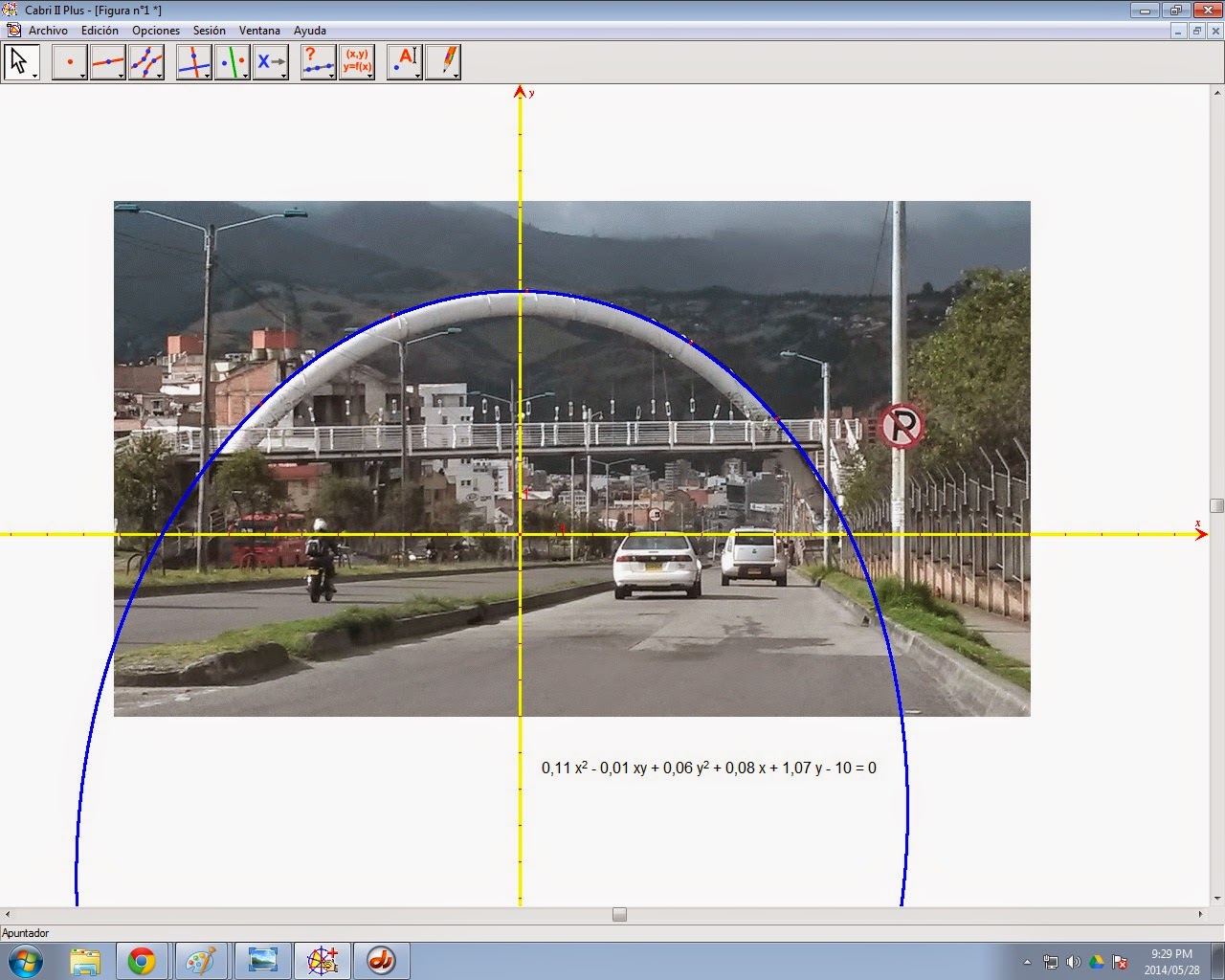
En mi ciudad, San Juan de Pasto - Colombia, hay un puente peatonal al cual se lo conoce con el nombre del PUENTE DEL CHORIZO. Una forma fácil de determinar la ecuación que describe al arco es trabajar en el software de Geometría Dinámica CABRI II PLUS. Se inserta la fotografía seleccionada en el área de trabajo de Cabri, mediante botón derecho. Con la opción PUNTO, se trazan cinco puntos a lo largo del arco. Utilizando la herramienta CÓNICA, se seleccionan los cinco puntos, obteniendo la cónica que más se ajusta a los puntos definidos, en este caso resultó una ELIPSE. Utilizando el comando COORDENADAS - ECUACIÓN, se determina la ecuación de la curva. !Listo! Fácil verdad? Didácticante hablando, éste es el primer paso para iniciar a los estudiantes en procesos de regresión. Es un paso de carácter intuitivo, previo al estudio formal del tema. Hasta pronto..... Espero fotografías de su ciudad con la respectiva cónica incluida. !Adios!

