MATE TICS

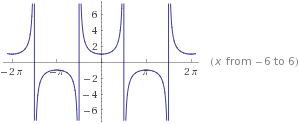
CÁLCULO Y GRAFICACIÓN  DE FUNCIONES TRIGONOMÉTRICAS INVERSAS La gráfica de la función secante, y = sec(x) = 1/cos(x) ,  es la siguiente: Nos interesa la función inversa de la secante, es decir: arc sec(x). En las calculadoras y en los computadores no se encuentra una tecla o combinación de ellas que permita su cálculo. Esta dificultad se supera sabiendo que: arc sec(x) = arc cos(1/x) Aprovechamos ésta relación para graficar arc sec(x), usamos el software GRAPES: Ahora simultaneamente las gráficas de sec(x) y arc sec(x): En la última gráfica se incluye la recta y = x, la cual es eje de simetría para dos funciones mutuamente inversas. Una manera de graficar la inversa de una función es aprovechar la simetría de éstas funciones. Veamos ahora arco cosecante (x): Como csc(x) = 1/sen(x), arc csc(x) = arc sin(1/x) Con base en esta identidad, graficamos en Derive:

Hoy buscando funciones trigonométricas inversas, de las cuales hallé algunas propiedades que desconocía, volví a encontrar dibujos por medio de ecuaciones, los cuales se hallan en el sitio WOLFRAM.COM. veamos: Ahora las pocas ecuaciones usadas para graficar: x (t) = ((-6 / 7 sin (22/15-13 t) sen -46/45 (11/10-10 t) -13 / 7 sin (16/11-3 t) -69/10 sin (17/12-2 t) 529/5 sin (t 11/7) 4/9 pecado (4 t 38/9) 32/7 sin (5 t 10/7) 4 / 3 sen (6 t 13/14) 25/4 sin (7 t 16/11) 9/7 pecado (8 t 10/11) 43/10 sen (9 t 17/12) + 7.3 pecado (11 t 22/5) 4/9 pecado (12 t 20/9) 81/5), theta (59 pi-t) theta (t-55 pi) + (-251/13 sin (11/8-3 t) 4100/11 sin (t 8/5) 31/9 sin (2 t 9/4) 17/12 pecado (4 t 22/5) 115 / 9 pecado (5 t 22/13) 24/11 pecado (6 t 9/2) 201/10 sen (7 t 17/10) 9/4 sin (8 t 13/5) + 112/11) theta (55 pi-t) theta (t-51 pi) + (507/5 sin (t 11/7) 1/5 sen (2 t 48/11) 73/10 sin ( 3 t 11/7) 23/10 sen (4 t 11/7) 1359/7), theta (51 pi-t) theta (t-47 pi) + (680/7 sin (t +11 / 7) 8/13 sin (2 t 23...

Comprender en que consiste resolver una ecuación y en particular trigonométrica, es posible por medio de la  representación gráfica de la ecuación, aspecto que se facilita con el advenimiento de las TICS matemáticas. Una vez visualizada la solución en forma gráfica, sigue el reto para el aprendiz resolverla a la buena usanza de lápiz y papel. Un ejemplo: Resolver la ecuación trigonométrica: 2*tg(x) - 3*cot(x) - 1 = 0 Solución gráfica en WOLFRAM.COM: Dar click al link: http://www.wolframalpha.com/input/?i=2+*tan(x)-3*cot(x)-1%3D0 La solución la conforman los puntos marcados en el eje X. Otro ejemplo: Resolver la ecuación trigonométrica: Se ingresa la expresión en WOLFRAM.COM, dar click al enlace: http://www.wolframalpha.com/input/?i=cos+%28x%29+%5E+2+-3*sen%28x%29%5E2%3D0 Se VE claramente la solución: 0.5 y -0.5. Una imágen dice más que mil palabras!