REPRESENTACIONES SEMIOTICAS DEL VOLUMEN MÁXIMO DE UNA CAJA
En esta entrada revisaremos un problema típico del calculo diferencial: Hallar el volumen máximo de una caja construida a partir de una lámina de largo y ancho determinados, recortando cuadrados en los vértices para formar la caja, la cual no tiene tapa.
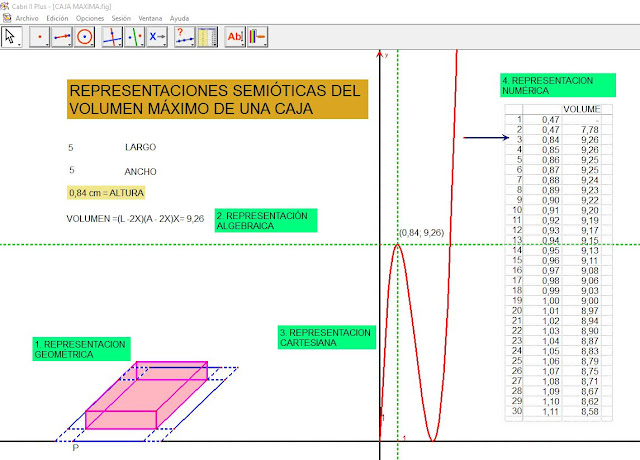
PASO 1. REPRESENTACIÓN GEOMÉTRICA
Aprovechando el entorno del Software CABRI II PLUS, se modela la caja, partiendo de un cuadrado proyectado en forma oblicua. Se define en el cuadrado un punto P del cual va a depender toda la construcción. Con la distancia de P al vértice próximo, se construyen cuadrados en los cuatro vértices, los cuales dependen del primero sobre P. En seguida se construye la caja uniendo los vértices internos de los cuadrados construidos sobre los vértices del cuadrado inicial. en este caso se usan las relaciones de paralelismo y perpendicularidad de los lados de la caja. De esta manera se obtiene una "caja dinámica", la cual al moverse el punto P, cambia de tamaño, pero conserva las relaciones implícitas en un paralelepípedo rectangular (Caja).
PASO 2. REPRESENTACIÓN ALGEBRAICA.
Para calcular el volumen de la caja, recordemos que se usa la expresión:
VOLUMEN = LARGO*ANCHO*ALTO, aplicado a este caso, resulta:
VOLUMEN = (L - 2X)*(A - 2X)*X
En la figura L = 5 cm, A = 5 CM, ALTURA = 0,84.
El Largo y el Ancho son variables, se puede modificar su valor. La altura es la distancia del punto P al vértice más cercano, la cual es variable y hace de X (variable independiente) en la construcción.
El resultado del volumen es un valor dinámico, es decir cambia según cambien el Largo, Ancho o Altura. Este resultado se usa para la siguiente representación:
PASO 3. REPRESENTACIÓN CARTESIANA
Para representar en el plano cartesiano la expresión que permite calcular el volumen de la caja en función de la distancia X, se transfieren las medidas de X al eje horizontal y el valor del volumen V al eje vertical, se levantan perpendiculares sobre los ejes y en estos valores y el punto de corte define el lugar geométrico asociado a la expresión algebraica del volumen. Se obtiene así la representación cartesiana propia de una función polinómica de tercer grado, la cual contiene el punto MÁXIMO que da respuesta al problema.
PASO 4. REPRESENTACIÓN NUMÉRICA
CABRI II PLUS, tiene una opción que permite construir una Tabla de Valores o Representación Numérica del modelo, en el cual se relaciona la longitud X con el volumen V.
SOLUCIÓN DEL PROBLEMA:
- Regresando a la primera representación, la Geométrica, al mover el punto P, se modifica el tamaño de la caja y se puede observar intuitivamente en que momento se tiene la caja más "grande". Sin embargo existe cierta dificultad en determinar en que momento sucede lo buscado.
La gráfica del medio es la solución.
La representación geométrica también se la puede trabajar construyendo cajas de cartón de diferentes tamaños para identificar la de volumen máximo:
Determinar la caja de mayor volumen de forma directa genera algunas controversias entre los alumnos, pero apoyandose en el valor numérico del volumen se determina en forma más aproximada la respuesta. En este caso, la caja del medio se acerca ala respuesta.
- La segunda representación, la algebraica, al generar el resultado del volumen cambiante en cada instante, permite identificar claramente cuando el volumen de la caja es el máximo.
- La tercera representación, la Cartesiana muestra la solución al ubicar el punto máximo de la curva. En las siguientes imágenes se observan tres instantes, de los cuales el intermedio da el valor máximo en forma aproximada:
- La cuarta representación, la numérica, muestra los valores de X y del volumen V, donde es fácil determinar donde están los valores máximos de X y el Volumen V. En la siguiente figura, en las columnas segunda y tercera respectivamente, se observan valores menores, de máximo y mayores:
CONCLUSIONES:
- RAYMOND DUVAL (autor de: Semiosis y Pensamiento Humano), plantea que tres representaciones semióticas de un objeto matemático son necesarias para su comprensión, en este ejemplo se han construido 4 representaciones semióticas.
El análisis de cada representación permite determinar la solución, pero su interrelación hace mejor la comprensión.
De igual manera tomando como referencia a DAVID TALL (Investigador Inglés del aprendizaje de las Matemáticas mediado por las tecnologías computacionales), se tienen representaciones CORPORIZADAS (Gráficas) y SIMBÓLICAS (Expresiones algebraicas) del problema, lo cual garantiza la comprensión
¿Qué sigue?
Es este el momento de resolver el problema recurriendo a la Tecnología Simbólica que provee la matemática para estos problemas: Utilización de la derivada para determinar los máximos y mínimos de una función.
REPRESENTACIÓN ANALÍTICA
REPRESENTACIÓN ANALÍTICA
Por lo tanto la solución al problema inicial se encuentra cuando X = 0.83 cm. en cuyo caso el VOLUMEN V = 9.25
- Finalmente podemos decir que el trabajo con las diferentes representaciones semióticas de un problema matemático aportan en la comprensión del problema, como también en el hallazgo de la solución. De igual manera la utilización de tecnología convencional y computacional favorecen un trabajo más eficiente y claro en la solución de problemas.
APRECIADOS LECTORES:
!FELIZ AÑO Y HASTA PRONTO!
















Comentarios
Publicar un comentario