GEOMETRÍA HIPERBÓLICA PRIMERA PARTE

-
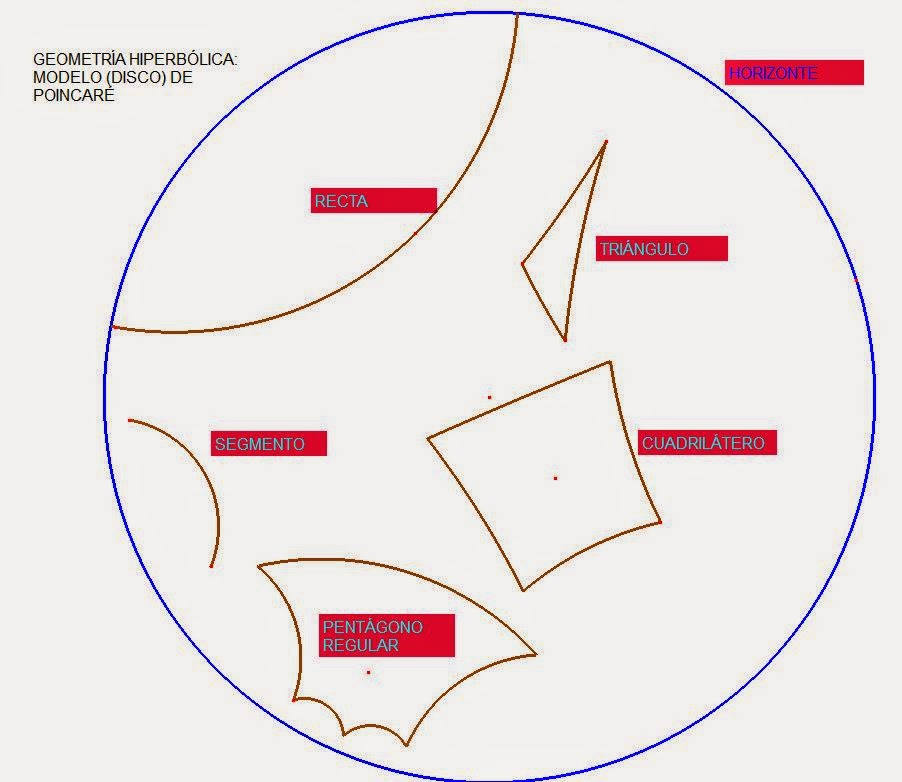
La mayoría estudiamos en el colegio geometría, llamada EUCLIDIANA, pero no es la única geometría existente, hay otras, entre ellas está LA GEOMETRÍA HIPERBÓLICA. con base en una extensión de CABRI II PLUS, he representado algunos elementos geométricos básicos en esta geometría: RECTAS, SEGMENTOS, TRIÁNGULOS, CUADRILÁTEROS Y PENTÁGONOS REGULARES.


Las anteriores representaciones adquieren sentido si asumimos que vivimos en una superficie esférica, donde por supuesto los elementos arriba mencionados cambian de la forma tradicional en que los conocemos.

Ahora una Parábola Hiperbólica:


Para la construcción, el programa pide: Directríz (arco), Foco (punto) y Círculo de referencia (Círculo de Poincaré)

Además el software da la ecuación:

 
Como se puede observar por la extensión de la ecuación hubo necesidad de recortarla.

ELIPSE HIPERBÓLICA

Nuevamente, Cabri permite graficar elipses, aquí se incluye el círculo referencial, las elipses y sus ecuaciones. !Maravilloso!

 HIPÉRBOLA HIPERBÓLICA

La hipérbola hiperbólica se grafica con base en los focos F1, F2, un punto de la curva P y el círculo de Poincare.

H CIRCLE - CÍRCULO HIPERBÓLICO


En la gráfica se observan dos H-círculos, la diferencia con los círculos euclidianos serían los radios: Se observa claramente que la longitud euclidiana de los radios en una circunferencia no es igual.

Por ahora suficiente. Ya ampliaré el tema.

Hasta pronto...

Comentarios

Publicar un comentario

Entradas populares de este blog

Cómo ganarse el BALOTO, matemáticamente?

-
Imagen
Hoy hablaré de juegos, en particular uno de moda: el BALOTO. El BALOTO, se juega apostando a 6 números, desde el 1 al 45. la Probabilidad, rama de las matemáticas, tiene el algoritmo para determinar la posibilidad de ganar, el cual consiste simplemente en dividir el NÚMERO DE CASOS FAVORABLES , entre el NÚMERO DE CASOS POSIBLES . Un caso típico es el lanzamiento de una moneda: La posibilidad de que caiga CARAS, es 1/2, es decir, 1 caso favorable / 2 casos posibles = 1/2 = 0,5 Examinemos el BALOTO: Se deben escoger 6 números, entonces: - Para el primer número hay 45 opciones de elegir un número. - Para el segundo número, hay 44 opciones de escogencia, porque no pueden repetirse. - Para el tercer número, hay 43 opciones. - Para el cuarto, hay 42 opciones. - Para el quinto, hay 41 opciones. - Para el sexto 40 opciones. Para conocer el número total de opciones se aplica el PRINCIPIO GENERAL DEL CONTEO : Se mu
Leer más

NAVIDAD Y SIMETRÍA

-
Imagen
SIMETRÍA CON GEOMETRÍA DINÁMICA En GOOGLE+, en la sección TICS EN LA EDUCACIÓN, se plantea la siguiente actividad: Naturalmente es un ejercicio sencillo, pero es susceptible de abordar desde diferentes frentes: - A lápiz y papel - En un software de graficación básico - En un software de Geometría Dinámica, por ejemplo CABRI II PLUS!. Dentro de este programa se puede desarrollar la actividad desde diferentes niveles de dificultad y aplicando diferentes estrategias, veamos: a) Nivel intuitivo: Insertando la figura en Cabri y con las herramientas básicas de polígono, segmento, rellenar color se puede resolver la actividad: b) Construir en Cabri la porción original del árbol, aplicar el concepto de simetría central o axial. Aquí se utilizó rectas perpendiculares y circunferencias, elementos que garantizan la simetría. En las tres gráficas últimas se ve el proceso de construcción, el cual recurre a diferentes conceptos geométricos básicos pero
Leer más

VARIANTES TEOREMA DE PITÁGORAS

-
Imagen
El Teorema de Pitágoras es muy famoso y de gran aplicación. Todos lo recuerdan de su bachillerato. Al menos dicen haber oído hablar de él, aunque no lo recuerdan al detalle. En Wikipedia, se encuentra el siguiente resultado: Pero éste es uno de muchos resultados interesantes de ésta propiedad geométrica. Lo interesante es que si en vez de cuadrados, se construyen semicírculos, la propiedad se mantiene: El semicírculo A1, es la suma de las áreas de los semicírculos A2 y A3!. La siguiente construcción se ha realizado en CABRI II PLUS, programa de geometría dinámica, que permite evidenciar en forma situada las propiedades matemáticas que se deseen estudiar. Lo interesante es que se pueden cambiar las dimensiones con un simple arrastre - draging y ver que las propiedades se mantienen. Lo mismo sucede si se construyen triángulos equiláteros en cada lado del triángulo original: El área del triángulo equilátero A1, es igual a la suma de los triángulos equiláteros A2 y A3.
Leer más