FUNCIÓN CUADRÁTICA DINÁMICA

El software de Geometría Dinámica, CABRI II PLUS, permite graficar todo tipo de función en forma dinámica, es decir se pueden manipular los elementos de la gráfica y analizar el comportamiento de los mismos.

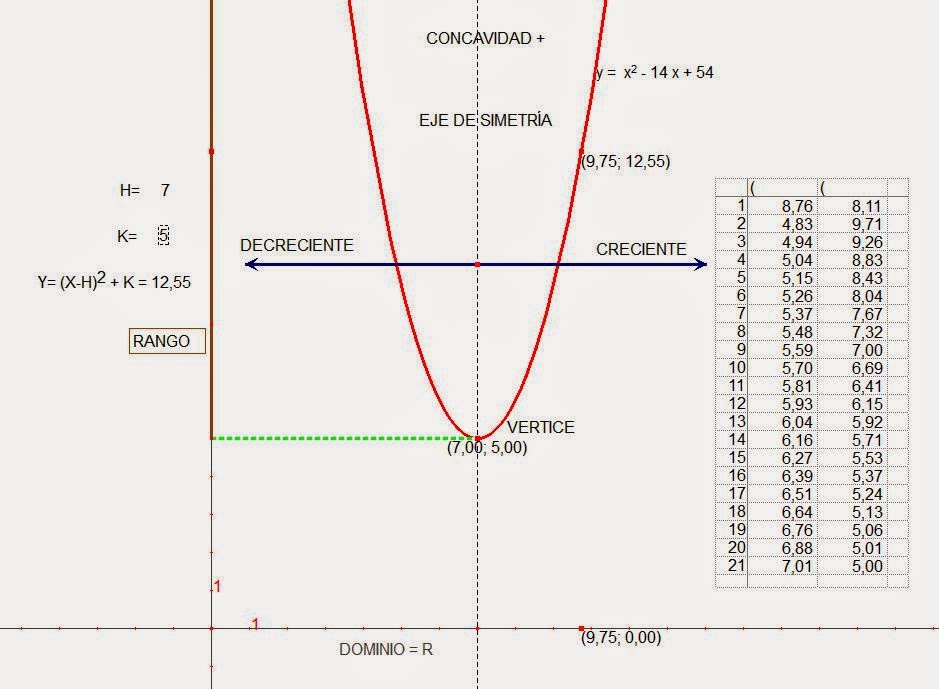
En la gráfica se ven las tres representaciones de la función: 

Analítica - ecuación

Gráfica - Cartesiana

Numérica - Tabla de valores

De igual manera se han incluido algunos elementos principales de la función.

La gráfica se construye a partir de un punto en el eje X y sus coordenadas (9.75, 0). 

A la abscisa se le hace corresponder mediante la opción CALCULADORA, la expresión analítica asociada a la función, en este caso cuadrática (Y=(X - H)¨2 + K). En esta ecuación, H = 7 y K=5, son valores arbitrarios, los cuales se convierten en el vértice de la parábola. Este ultimo resultado se traslada al eje Y (12,55). 

Por la abscisa y ordenadas marcadas en los ejes se trazan perpendiculares a los ejes y se obtiene el punto de coordenadas (9.75, 12.55). Este punto al moverse la abscisa por eje X, genera la parábola. Esto se logra con la opción Cabri: LUGAR.

Hasta aquí la construcción, lo demás es carpintería.

La TABLA DE VALORES se construye con la opción de Cabri: TABLA, apoyándose en la opción animación.

La ventaja de ésta construcción, sobre la tradicional de lápiz y papel es que al modificar únicamente los valores de H y K, se logra la representación de infinitas parábolas con el vértice (H, K). Este aspecto hace que el estudiante mediante la variación de H y K, observe los cambios en la gráfica y concluya sobre los mismos.

Cualquier otra función se pude abordar de igual manera.

CABRI, tiene una versión gratuita que se puede bajar de Internet y explorar con ella.

Invito a mis lectores a explorar la potencia de un software de geometría dinámica y así mejorar sus conocimientos geométricos y por que no matemáticos. Otro programa que utiliza el mismo enfoque es GEOGEBRA, el cual es totalmente libre.

HASTA PRONTO!