LÍMITE DE UNA FUNCIÓN DESDE LA GEOMETRÍA
ENFOQUE GEOMÉTRICO
DEL LÍMITE DE UNA FUNCIÓN
El estudio del concepto de LÍMITE DE UNA FUNCIÓN, resulta algo complicado desde su versión analítica, razón por la cual iniciar este tema desde un enfoque más CORPORIZADO, desde la geometría, resulta conveniente para docentes y estudiantes.
Las siguientes actividades ha sido recreadas y adaptadas para iniciarse en el estudio del tema de límites.
ACTIVIDAD
1.
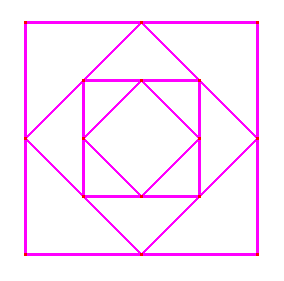
Se tiene un cuadrado de lado L. Se inscribe en el un cuadrado uniendo los
puntos medios de cada uno de sus lados. En el nuevo cuadrado se repite el
procedimiento de inscribir otro cuadrado. Este procedimiento se realiza
reiteradamente.
Utilizando recursos tradicionales (papel, lápiz, reglas, compás, etc.) y/o recursos computacionales (CABRI II PLUS, GEOGEBRA, DERIVE, Recursos en línea)
a) Representar gráficamente los
4 primeros cuadrados.
b) Calcular el área de cada uno
de los cuadrados
c) Generalizar los resultados,
para un cuadrado que ocupe el puesto n.
d) Elaborar una tabla de
valores que contenga el puesto n y su área.
e) Construir una gráfica
cartesiana que relacione n y área.
f) Con base en las diferentes
representaciones de la secuencia, argumentar a que resultado se acerca el área,
a medida que n crece.
g) Expresar el resultado
anterior como el límite de una función.
ACTIVIDAD
2.
Idéntico proceso se puede realizar a partir de triángulos equiláteros de lado L.
ACTIVIDAD
3.
Consultar construcciones similares a los anteriores y desarrollarlas.
!ESPERO RESPUESTAS!



Comentarios
Publicar un comentario